Quyền lợi thành viên thường & thành viên Vip
| Thành viên thường |
Thành viên VIP |
|
|---|---|---|
| Học và làm bài tập | 3 - 5 bài miễn phí (chọn sẵn) | Tất cả (không giới hạn) |
| Xem đáp án, lời giải chi tiết | ||
| Làm bài kiểm tra | Tất cả (không giới hạn) | |
| Toán vui mỗi ngày | ||
| Toán vui mỗi tuần | ||
| Thi đấu kiến thức | Không giới hạn | |
| Hỏi đáp nhanh | ||
| Danh sách bạn bè | Tối đa 50 bạn | Tối đa 200 bạn |
| Xem bài giảng video (Sắp ra mắt) |
Xem toàn bộ, không giới hạn |
|
| Phí thành viên |
Free | 200.000 đ/năm |
| ĐĂNG KÝ VIP |
Thành viên VIP sẽ được hưởng tất cả các quyền lợi VIP trong vòng 1 năm (365 ngày).
(học được tất cả các lớp, tất cả các môn có trên website)
(học được tất cả các lớp, tất cả các môn có trên website)
Hỏi đáp Toán lớp 9 - câu hỏi số 7881
a) Vẽ đồ thị các hàm số y=xy=x và y=2x+2y=2x+2 trên mặt phẳng tọa độ.b) Gọi AA là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm AA.c) Vẽ qua điểm B(0;2)B(0;2) một đường thẳng song song với trục OxOx, cắt đường thẳng y=xy=x tại điểm CC. Tìm tọa độ của điểm CC rồi tính diện tích tam giác ABCABC (đơn vị đo trên các trục tọa độ là xentimét).
Câu hỏi Toán lớp 9
Học và làm bài tập Toán lớp 9
Trả lời câu hỏi này
Lời giải chi tiết
a) +) Hàm số y=x:
Cho x=1⇒y=1⇒M(1;1)
⇒ đồ thị hàm số y=x là đường thẳng đi qua gốc tọa độ O và điểm M(1;1).
+) Hàm số y=2x+2
Cho x=0⇒y=2.0+2=2⇒B(0;2).
Cho x=−1⇒y=2.(−1)+2=−2+2=0⇒(−1;0)
Đồ thị hàm số y=2x=2 là đường thẳng đi qua hai điểm có tọa độ là B(0;2) và (−1;0).
Đồ thị như hình bên.
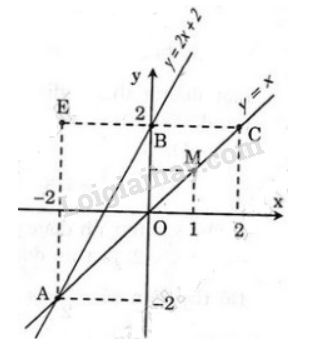
b) Tìm tạo độ giao điểm A:
Hoành độ giao điểm A là nghiệm của phương trình:
x=2x+2,
⇔x−2x=2
⇔−x=2
⇔x=−2
Thay x=−2 vào công thức của một trong hai hàm số trên ta được: y=−2
Vậy tọa độ cần tìm là: A(−2;−2).
c) +) Tìm tọa độ điểm C
Đường thẳng qua B(0;2) song song với trục hoành có phương trình là y=2 nên yC=2
Vì C cũng thuộc đường thẳng y=x nên hoành độ C là xC=2.
Vậy ta có tọa độ điểm C(2;2)
+) Tính diện tích tam giác ABCABC:
Kẻ AE⊥BC, dễ thấy AE=4.
Tam giác ΔABC có AE là đường cao ứng với cạnh BC.
Diện tích tam giác ΔABC là:
S=1212.AE.BC=1212.4.2=4(cm2.
Phương pháp giải
a) Cách vẽ đồ thị hàm số y=ax+b, (a≠0): Đồ thị hàm số y=ax+b(a≠0) là đường thẳng:
+) Cắt trục hoành tại điểm A(−ba;0).
+) Cắt trục tung tại điểm B(0;b).
Xác định tọa độ hai điểm A và B sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số y=ax+b(a≠0).
b) Đồ thị hàm số y=ax và y=a′x+b′ cắt nhau tại A thì hoành độ điểm A là nghiệm của phương trình: ax=a′x+b′. Giải phương tình tìm x, rồi thay vào một trong hai công thức hàm số trên tìm được tung độ điểm A.
c) +) Đường thẳng đi qua điểm B(0;b) song song với trục Ox có phương trình là: y=b.
+ Diện tích tam giác ABC: S=12.h.a
với h là độ dài đường cao, a là độ dài cạnh ứng với đường cao.
2 bình chọn đúng
Báo cáo sai phạm
duy1234567892007 đã chọn câu trả lời này
Lời giải chi tiết
a) +) Hàm số y=x:
Cho x=1⇒y=1⇒M(1;1)
⇒ đồ thị hàm số y=x là đường thẳng đi qua gốc tọa độ O và điểm M(1;1).
+) Hàm số y=2x+2
Cho x=0⇒y=2.0+2=2⇒B(0;2).
Cho x=−1⇒y=2.(−1)+2=−2+2=0⇒(−1;0)
Đồ thị hàm số y=2x=2 là đường thẳng đi qua hai điểm có tọa độ là B(0;2) và (−1;0).
Đồ thị như hình bên.

b) Tìm tạo độ giao điểm A:
Hoành độ giao điểm A là nghiệm của phương trình:
x=2x+2,
⇔x−2x=2
⇔−x=2
⇔x=−2
Thay x=−2 vào công thức của một trong hai hàm số trên ta được: y=−2
Vậy tọa độ cần tìm là: A(−2;−2).
c) +) Tìm tọa độ điểm C
Đường thẳng qua B(0;2) song song với trục hoành có phương trình là y=2 nên yC=2
Vì C cũng thuộc đường thẳng y=x nên hoành độ C là xC=2.
Vậy ta có tọa độ điểm C(2;2)
+) Tính diện tích tam giác ABCABC:
Kẻ AE⊥BC, dễ thấy AE=4.
Tam giác ΔABC có AE là đường cao ứng với cạnh BC.
Diện tích tam giác ΔABC là:
S=\(\frac{1}{2}\).AE.BC=\(\frac{1}{2}\).4.2=4(cm2.
Phương pháp giải
a) Cách vẽ đồ thị hàm số y=ax+b, (a≠0): Đồ thị hàm số y=ax+b(a≠0) là đường thẳng:
+) Cắt trục hoành tại điểm A(−ba;0).
+) Cắt trục tung tại điểm B(0;b).
Xác định tọa độ hai điểm A và B sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số y=ax+b(a≠0).
b) Đồ thị hàm số y=ax và y=a′x+b′ cắt nhau tại A thì hoành độ điểm A là nghiệm của phương trình: ax=a′x+b′. Giải phương tình tìm x, rồi thay vào một trong hai công thức hàm số trên tìm được tung độ điểm A.
c) +) Đường thẳng đi qua điểm B(0;b) song song với trục Ox có phương trình là: y=b.
+ Diện tích tam giác ABC: S=12.h.a
với h là độ dài đường cao, a là độ dài cạnh ứng với đường cao.
Xem thêm tại: http://loigiaihay.com/bai-16-trang-51-sgk-toan-9-tap-1-c44a4331.html#ixzz5I5J4sxgl
0 bình chọn đúng
Báo cáo sai phạm
Bạn hãy đăng ĐĂNG NHẬP mới được thực hiện tính năng này
Bạn cần giúp đỡ ?
